Đạo hàm chính là một phần kiến thức quan trọng không chỉ ở cấp trung học phổ thông mà ngay cả các sinh viên đang theo học ở các trường Đại học, Cao Đẳng cũng cần sử dụng. Nhưng vận dụng nhiều nhất có lẽ là các bạn học sinh lớp 11 và 12 Nếu bạn đã lỡ quên hoặc đang lơ mơ về kiến thức cùng bảng đạo hàm thì hãy nhanh chóng bổ sung ngay những quy tắc cơ bản giúp bạn vượt qua rất nhiều bài khó sau đây.

Những kiến thức cơ bản cần nhớ về đạo hàm
Trước hết chúng ta cần làm rõ khái niệm Đạo hàm là gì?
Đạo hàm là một khái niệm khá quen thuộc của toán học thuộc về giải thích. Nói về định nghĩa chung, đạo hàm của một hàm số chính là cách diễn tả sự biến thiên của một hàm số tại bất kì một điểm chưa xác định. Là một phép toán ngược với tích phân, đạo hàm được sử dụng rất nhiều trong các bài toán giải tích hiện nay. Nếu bạn không thực sự hiểu đạo hàm là gì thì khó có thể hiểu được bảng công thức đạo hàm nhắc tới ở phần sau.
Vì là biểu hiện cho sự biến thiên của hàm số nên hình thái của đạo hàm trong hình học chính là hệ số góc của hai đơn vị tiếp tuyến cùng với đồ thị hàm số. Như vậy, nếu bạn mạnh kiến thức trong phần đồ thị hàm số thì bạn sẽ hiểu nhanh hơn rất nhiều về đạo hàm.
Định nghĩa đạo hàm của một biến số
Giải thích về định nghĩa đạo hàm của một biến số thì chúng ta giả sử có một hàm số y = f (x). Hàm số này xác thực trong khoảng là (a;b) kèm với điều kiện là khoảng (a;b) này = x∈R | a<x<b .
Xét lấy giá trị của x0 ∈ (a;b) và giá trị của x ∈(a;b) và x ≠ x0
Nếu ta lần lượt quy đổi ∆x=x- x0 và ∆y=f x0+ ∆x-f(x0) thì đạo hàm biểu thị bằng công thức:
F‘(x)= fx0+ ∆x-f(x0)∆x= ∆f(x0)∆x
Trong đó, ∆x được gọi là đối số và ∆y được gọi là số gia hàm số. Ở đây ta xét đến tỷ số yx khi ∆x →0 sẽ tiến dần đến một giới hạn. Giới hạn này chính là đạo hàm.
Những quy tắc và cách tính đạo hàm bằng định nghĩa
Sau khi bạn đã nắm chắc được định nghĩa của đạo hàm, hiểu được ý nghĩa của nó thì bạn có thể dựa vào đó để tính được đạo hàm. Đây là cách tính cơ bản thường được áp dụng trong hầu hết các bài tính đơn giản, và cũng là nguyên tắc đầu tiên để phát triển lên các cấp độ khó hơn sau này.
Quy tắc cơ bản bạn cần nắm rõ khi tính đạo hàm như sau:

Các quy tắc trên nhìn có vẻ lằng nhằng nhưng khi bạn tiếp xúc và làm nhiều sẽ thấy khá đơn giản, dễ hiểu và dễ nhớ. Đây đều là những quy tắc sẽ được dùng thường xuyên trong các cách tính đạo hàm bằng máy tính hay bằng tay.
Trong Toán học xuất hiện khá nhiều loại hàm số và mỗi loại hàm số lại có cách tính đạo hàm riêng, vì vậy nếu bạn thuộc hết các cách tính đạo hàm này thì các bài toán giải tích trở nên dễ dàng hơn rất nhiều. Bảng đạo hàm cơ bản cũng khá dễ nhớ và được sử dụng nhiều vì vậy không quá khó khăn để ghi nhớ. Sau đây là bảng công thức đạo hàm đầy đủ cho những hàm số cơ bản hay gặp nhất.

Lưu ngay bảng đạo hàm này về và bạn đã có một phần của cuốn bách khoa toàn thư tích phân rồi đấy.
Định nghĩa và bảng đạo hàm lượng giác
Đạo hàm của các hàm lượng giác có hơi khác với đạo hàm của hàm số thông thường. Đây là một phương pháp được sử dụng để tìm tốc độ biến thiên của các hàm số lượng giác, tốc độ biến thiên này dựa trên sự biến thiên của biến số. Thông thường thì các hàm số lượng giác mà ta hay gặp trong các bài toán là sin(x), cos(x) và tan(x).
Muốn biết được đạo hàm của hầu hết các hàm số lượng giác thì chúng ta nên biết được đạo hàm của 2 hàm cơ bản nhất là hàm sin(x) và cos(x). Lý do là vì các hàm số lượng giác khác đều có thể quy đổi về hai hàm cơ bản này. Dưới đây có liệt kê ra những đạo hàm rất hay gặp nếu bạn có một đề bài về hàm số lượng giác. Thông thường bạn chỉ cần áp dụng 4 trường hợp đầu tiên mà thôi vì những hàm lượng giác sau đó cũng khá hiếm trong các bài toán thông thường hiện nay.
=> List nhạc giúp bạn tập trung tinh thần để học tập tại đây
Hướng dẫn cách chứng minh đạo hàm của hai hàm cơ bản sin và cos
Giới hạn của sin khi θ →0
Bằng đầu bằng một hình tròn có bán kính bằng r như hình bên dưới. Lúc này giả sử gọi là góc tại tâm O tạo bởi 2 đường OA và OK. Do khi trước chúng ta đã giả định θ tiến dần tới 0, nên có thể nói là θ sẽ là một số dương rất nhỏ thỏa mãn điều kiện 0 < θ ≪ 1.
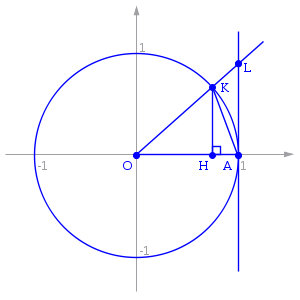
Gọi R1, R2, R3 lần lượt là diện tích của OAK, hình quạt OAK, OAL thì sẽ có (R1) < (R2) < (R3). Sau khi tính được các diện tích bằng hàm lượng giác chúng ta có:
R1<R2<R3↔ 12r2sin < 12r2θ< 12r2tan
Sau đó dựa vào định lý kẹp chúng ta sẽ rút ra được: sin = 1
Tương tự với cách suy luận này chúng ta cũng áp dụng cho θ là số âm rất nhỏ tiến dần đến 0.
Bảng đạo hàm và nguyên hàm
Nói một cách dễ hiểu thì nguyên hàm là phép tính ngược lại với đạo hàm. Vì vậy để cho dễ nhớ thì thông thường người ta vẫn thường tổng hợp bảng đạo hàm mở rộng kèm với nguyên hàm để dễ nhớ và so sánh. Chúc các bạn thành công!
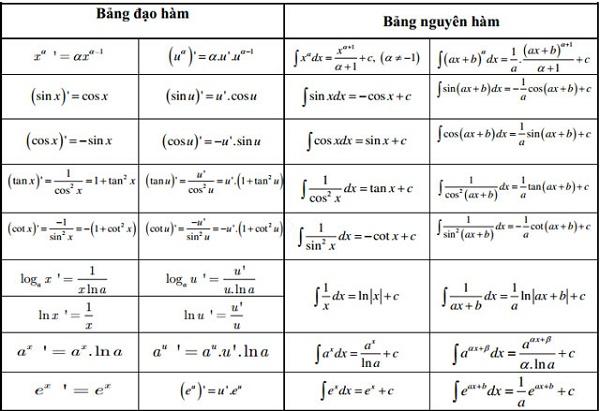
Ngoài ra còn có một số bảng đạo hàm cấp cao khác giúp các bạn dễ dàng hơn trong việc tìm ra công thức phù hợp cho bài toán đang gặp phải.

Bảng đạo hàm trên khá đầy đủ và tổng hợp được các kiến thức hcinhs mà mọi người cần nhớ khi làm toán về đạo hàm. Nắm chắc được các kiến thức này thì bạn chỉ việc tạo ra sự logic trong suy luận khi áp dụng vào các bài giải tích mà thôi. Đây là những thông tin hữu ích và các bảng tổng hợp giúp các bạn ôn tập khoa học hơn, đồng thời rút ngắn thời gian tra cưu công thức tính đạo hàm khi chưa thành thạo.
=> Top các trường Đại học có học phí thấp



