Hình học không gian là một phần khá khó nhằn trong Toán học mà các học sinh Trung học phổ thông phải đối mặt. Không chỉ là tính thể tích hình trụ, hình cầu, hình chóp… mà các em còn phải giải quyết các đề bài phức tạp hơn thế. Nhưng hãy bắt đầu từ những kiến thức cơ bản này trước đã, từ đó mới có thể làm được những bài nâng cao.
=> Môn Toán sẽ giải quyết việc ‘học vất vả song không để làm gì’

Định nghĩa về hình trụ
Trước tiên bạn cần nắm định nghĩa của hình trụ. Hình trụ tròn là hình có mặt đáy là hai hình tròn có diện tích bằng nhau và năm song song với nhau. Để minh họa rõ hơn thì bạn gặp rất nhiều hình trụ ngoài đời thật như lon nước ngọt, cái cốc, … Bởi vậy cách tính thể tích hình trụ không chỉ áp dụng được trong toán học mà còn có thể ứng dụng nhiều trong thực tế nữa.
=> Top kim loại cứng nhất hiện nay
Công Thức Tính Thể Tích Hình Trụ
Công thức này là công thức cơ bản mà bạn có thể tìm thấy trong bất cứ cuốn sách giáo khoa nào về hình học không gian. Tuy chỉ là công thức cơ bản và không quá phức tạp nhưng bạn vẫn cần thuộc và áp dụng thuần thục nó.
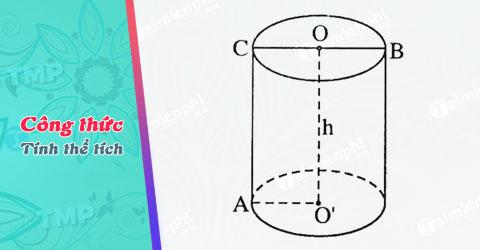
Nắm rõ công thức tính thể tích hình trụ để giải được tất cả các bài tập liên quan
Cách tính thể tích hình trụ tròn như sau : V = π. r2. h
Giải thích các kí hiệu trong công thức ta có:
V là kí hiệu thể tích hình trụ tròn mà ta đang cần tính
r là bán hình của một mặt đáy hình trụ ( phía trên chúng ta đã định nghĩa hình trụ có hai mặt đáy là hai hình tròn bằng nhau )
h là kí hiệu chiều cao của hình trụ
π là hằng số quy định ( π = 3, 14)
– Đơn vị thể tích của hình trụ ở đây được quy định là mét khối ( kí hiệu là m3)
Giải thích bằng lời cho công thức này khá đơn giản, nếu chúng ta muốn tính thể tích của hình trụ tròn thì lấy chiều cao của hình trụ nhân với bình phương của bán kính mặt đáy cùng số pi. Hoặc để hiểu đơn giản hơn thì bạn sẽ tính diện tích của mặt đáy rồi nhân theo chiều cao. Khá dễ hiểu phải không nào?
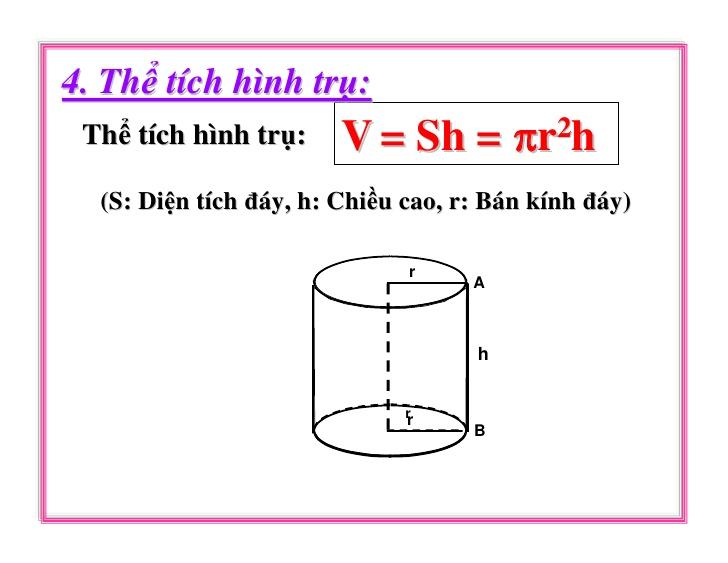
Tổng quát về công thức tính thể tích hình trụ tròn đơn giản và cơ bản nhất bạn nên học thuộc lòng
Để lấy một ví dụ minh họa cụ thể hơn: Yêu cầu tính thể tích hình trụ tròn biết các chỉ số sau đây: bán kính hai mặt đáy bằng 7,1 cm; chiều cao của hình trụ bằng 5 cm.
Hướng Dẫn cách giải : Bài toán này nếu nắm được công thức thì rất đơn giản, chỉ việc áp dụng các con số đã biết để tính toán là xong. Cụ thể thay r = 7.1 và h = 5 ta có:
V = 3.14 x (7,1)2 x 5 = 791,437 ( đơn vị cm3)
Một số bài toán liên quan đến công thức tính thể tích hình trụ tròn và hướng dẫn cách giải
Yêu cầu tìm bán kính mặt đáy
Trong các bài toán về thể tích hình trụ thì yêu cầu tìm bán kính đày khá phổ biến và hay gặp phải. Nếu đã nắm rõ công thức thì không cần phải lo lắng lắm về đề bài này. Vì hai mặt đáy của hình trụ tròn bằng nhau nên bạn có thể tìm bất kì 1 trong 2 bán kính mặt đáy.
Nếu biết đường kính của mặt đáy hình tròn thì mọi việc quá đơn giản, chỉ cần lấy đường kính chia đôi sẽ ra bán kính. Nếu không biết chỉ số đường kính thì chúng ta dựa vào công thức khác, chẳng hạn như công thức tính thể tích hình lăng trụ đứng như trên. Nếu các chỉ số khác như thể tích hình trụ, chiều cao của hình trụ chúng ta đã biết hoặc có thể tính được thì có thể từ đó suy ra bán kính của mặt đáy
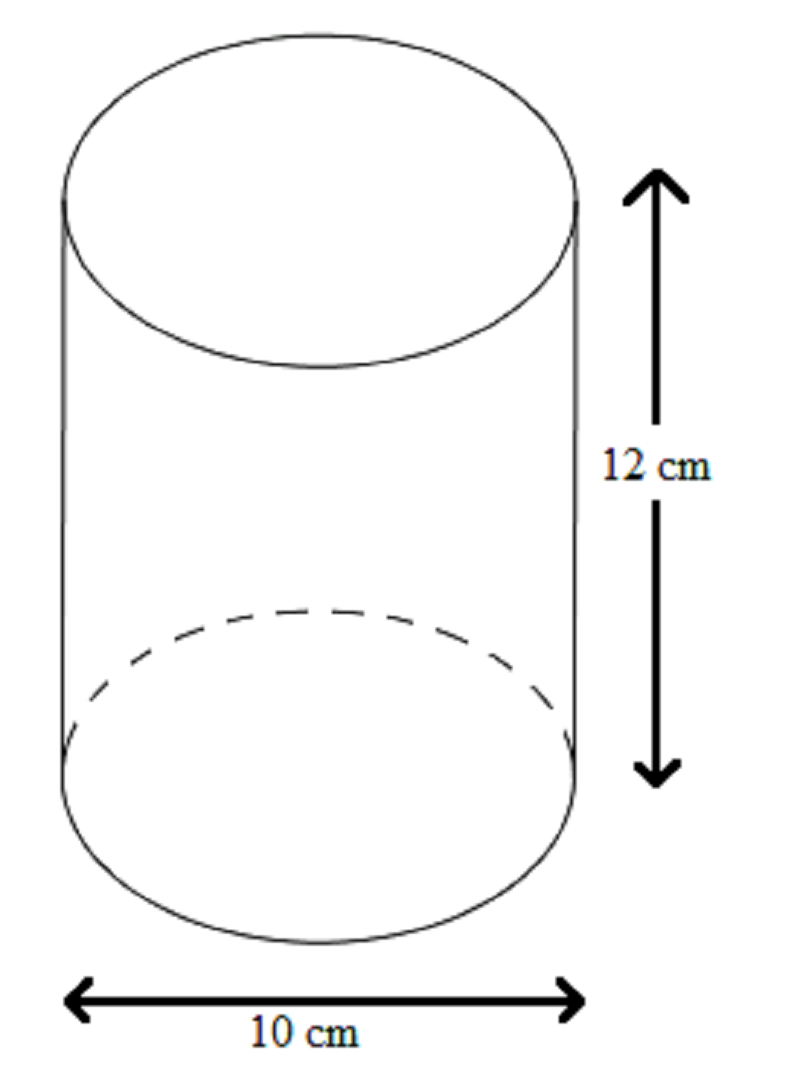
Công thức tính thể tích hình trụ tròn có thể áp dụng để tính ngược lại bán kính hình tròn mặt đáy
Tìm diện tích mặt đáy tròn của hình trụ
Tương tự như trên, nếu hcungs ta biết được bán kính hình tròn thì áp dụng ngay công thức A = π.r2 để tính diện tích mặt đáy ( A là kí hiệu của diện tích mặt đáy, r là bán kính và π là hằng số )
Ví dụ minh họa: Yêu cầu tính diện tích đáy tròn của hình trụ biết bán kính của nó bằng 6,5 cm.
Cách giải: Rất đơn giản khi bạn đã có sẵn công thức tính diện tích
=> Diện tích đáy tròn sẽ bằng: A = 3,14 x (6,5)2 = 132, 665 (cm2)
Tìm chiều cao của hình trụ tròn
Đây cũng là một yếu tố quan trọng hay gặp trong các bài toán về hình học không gian. Chiều cao này được định nghĩa là khoảng cách giữa hai mặt đáy của hình trụ. Chiều cao này xuất hiện trong khá nhiều công thức tính, ở đây chỉ đề cập đến những bài toán có liên quan đến thể tích hình trụ mà thôi.
Như đã nhắc ở đầu bài, ta có công thức tính thể tích hình trụ rỗng là: V = π. r2. H
Vậy để tính chiều cao của hình trụ trong điều kiện các chỉ số khác đã biết, ta sử dụng công thức:
H = V/ (π. r2) trong đó V là thể tích hình trụ và r là bán kính mặt đáy.
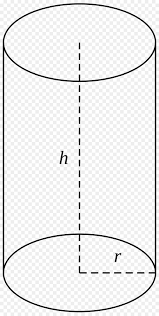
Chiều cao của hình trụ là khoảng cách giữa hai mặt đáy và có rất nhiều cách để tính được chiều cao này của hình trụ tròn
Công thức tính thể tích hình trụ tròn ở trên cũng khá dễ nhớ phải không? Công thức này là cội nguồn giúp chúng ta giải quyết được rất nhiều bài toán khó. Vì vậy đừng quên học thuộc nó và áp dụng nhuần nhuyễn trong các đề bài liên quan. Ngoài ra có thể tham khảo thêm các công thức tính thể tích không gian khác như thể tích hình trụ tam giác, thể tích hình cầu …. Để có thể dễ dàng giải quyết được nhiều loại đề bài hình học không gian hơn.
Để hình học không gian không còn là nỗi ám ảnh thì các bạn hãy nắm vững các kiến thức về hình học phẳng trước. Lối tư duy của hình học không gian cũng không quá khác biệt so với hình học phẳng. Chỉ cần các em nắm chắc hình học phẳng, từ đó tạo nên được không gian đa chiều cho hình học không gian dựa vào các công thức liên kết, hình học không gian sẽ trở nên dễ hiểu hơn rất nhiều.
=> Bảng công thức tính đạo hàm chuẩn từ A-Z



